Fast Fourier Transforms

by Don Cross - dcross@intersrv.com

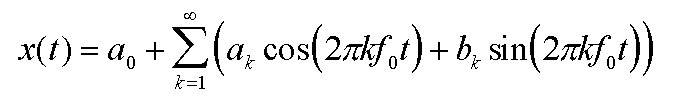
Last update to this page: 18 May 1998

Here are some prominent web sites which link to this FFT page:

Amara's Science Links
Embedded Systems Programming Magazine
Numeric section in the Turbo Pascal Programmers Page [uses frames].

C/C++ source code

fft.zip - [last update: 15 March 1998.]
This file contains C code I wrote for performing Fast Fourier Transforms (FFTs). This code is C++ callable also. My implementation is based on ideas from the book Numerical Recipes in Fortran by Press, Teukolsky, Vetterling, and Flannery, published by Cambridge University Press. [Note: There is a version of this book called Numerical Recipes in C which contains the same information with C source code instead of Fortran.]

This source code contains one implementation for arrays of type float and one for arrays of double. Both functions can perform the transform or the inverse transform, depending on a flag passed as a parameter.

fftdom.cpp - This is a sample C++ function which shows how to find the peak power frequency in the output arrays produced by the FFT. This function returns the frequency in Hz of the part of the frequency spectrum which has maximum power. Note that the returned value can actually be between the integer multiples of the Fourier base frequency f₀ = samplingRate / numSamples. This code calculates a weighted average of the power spectrum around the peak frequency, to more accurately determine the true peak frequency. This technique is similar to calculating the center of gravity of a horizontal beam with continuously varying linear density along its length.

Turbo Pascal source code

fourier.pas - [last update: 11 December 1996.]
Here is the Fast Fourier Transform algorithm in a Turbo Pascal unit. Use the procedure fft to perform the forward transform, and ifft for the inverse transform.

testfft.pas - This is a little test program for fourier.pas, which also serves as a demo of how to use the code.

testfft.zip - This zip file contains testfft.exe and egavga.bgi. Download this if you want to run the testfft program but do not have access to Borland's Turbo Pascal compiler.

A Tutorial on the Fast Fourier Transform

1. Introduction to digital audio

If you are already familiar with general digital audio concepts, you can skip this section.

The most common type of digital audio recording is called pulse code modulation (PCM). Pulse code modulation is what compact discs and most WAV files use. In PCM recording hardware, a microphone converts a varying air pressure (sound waves) into a varying voltage. Then an analog-to-digital converter measures (samples) the voltage at regular intervals of time. For example, in a compact disc audio recording, there are exactly 44,100 samples taken every second. Each sampled voltage gets converted into a 16-bit integer. A CD contains two channels of data: one for the left ear and one for the right ear, to produce stereo. The two channels are independent recordings placed "side by side" on the compact disc. (Actually, the data for the left and right channel alternate...left, right, left, right, ... like marching feet.)

The data that results from a PCM recording is a function of time. It often amazes people that a sequence of millions of integers on a compact disc recording can yield music and speech. People tend to wonder, "How can a stream of numbers sound like an entire orchestra?" It seems magical, and it is! Yet the magic is not in the digital recording; it's in your ear and your brain. To understand why this is true, imagine that you could place a microscopic movie camera in your ear to film your ear drum in slow motion. Suppose the movie camera was so fast that it could take a picture every 1/44,100 of a second. Also, suppose that the images this camera captured on film were so crisp and sharp that you could discern 65,536 (64K) distinct positions of the ear drum's surface as it moved back and forth in response to incoming sound waves. If you used this hypothetical technology to film your ear drum while listening to your best friend saying your name, then took the resulting movie and wrote down the numeric position of your ear drum in every frame of the movie, you would have a digital PCM recording. If you could later make your ear drum move back and forth in accordance with the thousands of numbers you had written down, you would hear your friend's voice saying your name exactly as it sounded the first time. It really doesn't matter what the sound is - your friend, a crowded party, a symphony - the concept still holds. When you hear more than one thing at a time, all the distinct sounds are physically mixed together in your ears as a single pattern of varying air pressure. Your ears and your brain work together to analyze this signal back into separate auditory sensations. It's literally all in your head!

2. Frequency information in a function of time

An organ in our inner ears called the cochlea enables us to detect tonality in the sounds we hear. The cochlea is acoustically coupled to the eardrum by a series of three tiny bones. It consists of a spiral of tissue filled with liquid and thousands of tiny hairs. The hairs on the outside of the spiral are longer than the hairs on the inside of the spiral. In fact, the hairs get gradually smaller as you wind your way around the spiral to the inside. Each hair is connected to a nerve which feeds into the auditory nerve bundle going to the brain. The longer hairs resonate with lower frequency sounds, and the shorter hairs with higher frequencies. Thus the cochlea serves to transform the air pressure signal experienced by the ear drum into frequency information which can be interpreted by the brain as tonality and texture. This way, we can tell the difference between adjacent notes on a piano, even if they are played equally loud. The Fourier Transform is a mathematical technique for doing a similar thing: resolving any time-domain function into a frequency spectrum, much like a prism splitting light into a spectrum of colors. This analogy is not perfect, but it gets the basic idea across.

3. The Fourier Transform as a mathematical concept

The Fourier Transform is based on the discovery that it is possible to take any periodic function of time x(t) and resolve it into an equivalent infinite summation of sine waves and cosine waves with frequencies that start at 0 and increase in integer multiples of a base frequency f₀ = 1/T, where T is the period of x(t). Here is what the expansion looks like:

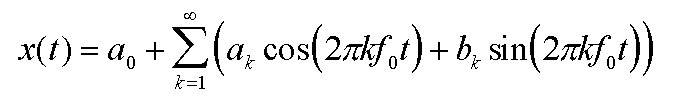
Fourier Series equation

An expression of the form of the right hand side of this equation is called a Fourier Series. The job of a Fourier Transform is to figure out all the a_k and b_k values to produce a Fourier Series, given the base frequency and the function x(t). You can think of the a₀ term outside the summation as the cosine coefficient for k=0. There is no corresponding zero-frequency sine coefficient b₀ because the sine of zero is zero, and therefore such a coefficient would have no effect.

Of course, we cannot do an infinite summation of any kind on a real computer, so we have to settle for a finite set of sines and cosines. It turns out that this is easy to do for a digitally sampled input, when we stipulate that there will be the same number of frequency output samples as there are time input samples. Also, we are fortunate that all digital audio recordings have a finite length. We can pretend that the function x(t) is periodic, and that the period is the same as the length of the recording. In other words, imagine the actual recording repeating over and over again indefinitely, and call this repeating function x(t). The math for the FFT then becomes simpler, since it will start with the base frequency f₀ which spans one wavelength over the width of the recording. In other words, f₀ = samplingRate / N, where N is the number of samples in the recording.

4. The Discrete Fast Fourier Transform algorithm

The discrete FFT is an algorithm which converts a sampled complex-valued function of time into a sampled complex-valued function of frequency. Most of the time, we want to operate on real-valued functions, so we set all the imaginary parts of the input to zero. If you want to use my source code, here are some things you need to know.

Your input arrays and output arrays all must have a common size, which we will call n.
The value of n must be a positive integer power of 2. For example, an array of 1024 is allowed, but one of size 1000 is not. The smallest allowed array size is 2. There is no upper limit to the value of n other than limitations inherent in memory allocation of the four arrays (input{real,imaginary}, output{real,imaginary}) and time limits inherent in executing this O(n*log(n)) algorithm.
The realOut array holds the coefficients of the cosine waves in the Fourier formula.
The imagOut array holds the coefficients of the sine waves in the Fourier formula.
The ordering of the frequencies in the output arrays (realOut and imagOut) are a little bit strange, because they contain both positive and negative frequencies. Both positive and negative frequencies are necessary for the math to work when the inputs are complex-valued (i.e. when at least one of the inputs has a non-zero imaginary component). Most of the time, the FFT is used for strictly real-valued inputs, and this is especially the case in digital audio analysis. The FFT, when fed real-valued inputs, gives outputs whose positive and negative frequencies are redundant. It turns out that they are complex conjugates of each other, meaning that their real parts are equal and their imaginary parts are negatives of each other. If your inputs are all real-valued, you can get all the frequency information you need just by looking at the first half of the output arrays.
The first slot of the output, realOut[0] and imagOut[0], contains the average value of all the input samples. For the output indicies i = 1, 2, 3, ..., n/2, the value of the frequency expressed in Hz is f = samplingRate * i / n. The negative frequency counterpart of every positive frequency index i = 1, 2, 3, ..., n/2 - 1, is i' = n - i. Here's an example. Suppose the sampling rate is 44,100 Hz, and we are using buffers of 1024 complex numbers for both the inputs and outputs. The frequency at i = 1 would be (44,100 Hz) * 1 / 1024 = 43.07 Hz. The negative frequency counterpart would be at i = 1024 - 1 = 1023 (i.e. the last slot in the array), with a frequency of -43.07 Hz. Likewise, i = 17 would correspond to a frequency of (43.07 Hz)*17 = 732.13 Hz, while i = 1024 - 17 = 1007 would correspond to -732.13 Hz, etc.
The index n/2 is a special case: it corresponds to the Nyquist frequency, which is always half the sampling rate in any digital PCM recording. For example, the Nyquist frequency in a CD audio recording is (44,100 Hz)/2 = 22,050 Hz. The Nyquist frequency is important because it is the highest frequency that a PCM digital audio recording can reproduce. Nothing above this frequency can be represented by PCM. If you try to sample a signal which is higher in frequency than the Nyquist frequency, severe distortion known as aliasing occurs, analogous to optical illusions of slow or backwards motion in films of wagon wheels in old Westerns. Recording engineers know that they have to filter out any signals above the Nyquist frequency in their analog equipment before the signals are digitally sampled, in order to avoid aliasing problems. Note that the Nyquist frequency limitation is inherent in the digital recording itself, whether or not an FFT is ever performed on the recording.
If the input to the FFT is real, the Nyquist frequency index n/2 in the output will always have a real value (meaning the imaginary part will be zero, or something really close to zero due to floating-point roundoff errors). This is because, using the formula above, i' = n - n/2 = n/2, so the Nyquist frequency is its own negative frequency counterpart. Therefore, it must equal its own complex conjugate, which in turn forces it to be a real number.
Sometimes you will be interested only in the magnitude of each frequency component, or its phase angle. Here is how you calculate each:
```
	#include <math.h>

	double magnitude = sqrt ( realOut[i]*realOut[i] + imagOut[i]*imagOut[i] );
	double angle = atan2 ( imagOut[i], realOut[i] );
```
If you are interested in doing the inverse conversion, from magnitude and angle to real and imaginary, use the following code:
```
	#include <math.h>

	double real = magnitude * cos(angle);
	double imag = magnitude * sin(angle);
```
If you need to have a rigorous mathematical understanding of the FFT, here is an equation which tells you the exact relationship between the inputs and outputs. In this equation, x_k is the kth complex-valued input (time-domain) sample, y_p is the pth complex-valued output (frequency-domain) sample, and n = 2^N is the total number of samples. Note that k and p are in the range 0 .. n-1.

Although this formula tells you what the FFT is equivalent to, this formula is not how the FFT algorithm is implemented. This formula requires O(n^2) operations, whereas the FFT itself is O(n*log₂(n)). In other words, if you were to use the formula above, it would be much slower than using the FFT algorithm. However, if you only need a small subset of the frequency spectrum (say two or three frequency samples), or you have a number of samples that isn't a power of 2, this formula combined with some trig optimizations could be of practical use. Note that I have done exactly this in my Turbo Pascal source code in a procedure called CalcFrequency.

5. Applications of the FFT

The FFT algorithm tends to be better suited to analyzing digital audio recordings than for filtering or synthesizing sounds. A common example is when you want to do the software equivalent of a device known as a spectrum analyzer, which electrical engineers use for displaying a graph of the frequency content of an electrical signal. You can use the FFT to determine the frequency of a note played in recorded music, to try to recognize different kinds of birds or insects, etc. The FFT is also useful for things which have nothing to do with audio, such as image processing (using a two-dimensional version of the FFT). The FFT also has scientific/statistical applications, like trying to detect periodic fluctuations in stock prices, animal populations, etc. FFTs are also used in analyzing seismographic information to take "sonograms" of the inside of the Earth. I have even read about Fourier methods used to analyze DNA sequences!

The main problem with using the FFT for processing sounds is that the digital recordings must be broken up into chunks of n samples, where n always has to be an integer power of 2. One would first take the FFT of a block, process the FFT output array (i.e. zero out all frequency samples outside a certain range of frequencies), then perform the inverse FFT to get a filtered time-domain signal back. When the audio is broken up into chunks like this and processed with the FFT, the filtered result will have discontinuities which cause a clicking sound in the output at each chunk boundary. For example, if the recording has a sampling rate of 44,100 Hz, and the blocks have a size n = 1024, then there will be an audible click every 1024 / (44,100 Hz) = 0.0232 seconds, which is extremely annoying to say the least.

I have had some success getting rid of the discontinuities using the following method. Assume the buffer size is n = 2^N. On the first iteration, read n samples from the input audio, do the FFT, processing, and IFFT, and keep the resulting time data in a second buffer. Then, shift the second half of the original buffer to the first half (remember that n is a power of 2, so it is divisible by 2), and read n/2 samples into the second half of the buffer. Do the same FFT, processing, IFFT. Now, do a linear fade out on the second half of the old buffer that was saved from the first (FFT,processing,IFFT) triplet by multiplying each sample by a value that varies from 1 (for sample number n/2) to 0 (for sample number n - 1). Do a linear fade in on the first half of the new output buffer (going linearly from 0 to 1), and add the two halves together to get output which is a smooth transition. Note that the areas surrounding each discontinuity are virtually erased from the output, though a consistent volume level is maintained. This technique works best when the processing does not disturb the phase information of the frequency spectrum. For example, a bandpass filter will work very well, but you may encounter distortion with pitch shifting.

Here is an example C++ program of the preceeding method. Notice especially how the functions FadeMix and ShiftData are called from main.

If you really want to do clean sounding algorithmic filters on digital audio, you should check out time-domain filters (also known as linear filters), which process the input audio samples one at a time, instead of processing blocks of samples.

Other FFT web sites

FFTW - The "Fastest Fourier Transform in the West" - developed at MIT by Matteo Frigo and Steven G. Johnson. Look here if you are interested in portable FFT source code for multi-dimensional analysis, or if you have buffer sizes which cannot be a power of two.
The Fourier Page by Douglas Nunn. Has lots of interesting links... some technical, some historical.
Public Domain FFT Code - Has public domain source code for Fortran and C. Also has a nice theoretical discussion of the continuous Fourier Transform, from which all Discrete Fourier Transforms are derived (including the FFT).
FFT for 2D matrices in Fortran by Hon W Yau, Bhaven Avalani and Alok Choudhary.

Miscellaneous

Amara's Wavelet Page - Has ample links to wavelet resources.
A Basis for Functions: The Fourier Series - Contains some fundamental background concepts.

[back to Digital Audio page]
[Don Cross home page]

Number of visits to this page:

If you want to add a counter to your web page, try Web-Counter.