Last update to this page: 14 January 1998
If you need to calculate both the sine and cosine of a steadily increasing angle, see the next two sections.
If you need only sines or cosines, but not both, you should see Section 4.

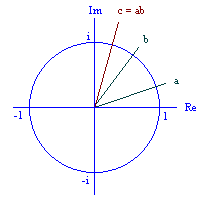
The geometric interpretation of complex number multiplication allows us to see how to rotate a complex number about the origin by merely multiplying it by another complex number. The payoff comes by calculating the product using the usual algebraic interpretation of complex number multiplication:
Re{c} = Re{a}Re{b} - Im{a}Im{b}
Im{c} = Re{a}Im{b} + Im{a}Re{b}
If we multiply two unit-length complex numbers together, the result will also have a magnitude of 1, but will have its angle shifted. We can do this repeatedly. We need to call trig functions for the starting angle and the increment angle to get things started. After that, we can just use floating point multiplication, addition, and subtraction. The real component of the complex number is the cosine of its angle, and the imaginary component is the sine. Note that both the sine and cosine are available on each iteration, whether or not you need both of them. Even if you need only one of them, this method is still dramatically faster than the equivalent trig functions calls.
Here's a little C program to illustrate this technique. This program prompts the user for both a starting angle a0 and an increment angle da. It then prints out a table of the sines and cosines of the first 20 angles a = a0 + k*da, where k = 0, 1, 2, ..., 19.
/* trig1.c - Example program by Don Cross <dcross@intersrv.com> */
/* http://www.intersrv.com/~dcross/fasttrig.html */
#include <stdio.h>
#include <math.h>
#define PI (3.14159265358979323846)
int main (void)
{
double a, da, a0_rad, da_rad;
double a_sin, a_cos, da_sin, da_cos;
double temp;
int k;
printf ( "Enter starting angle in degrees: " );
scanf ( "%lf", &a );
a0_rad = a * PI / 180.0; /* convert to radians */
printf ( "Enter increment angle in degrees: " );
scanf ( "%lf", &da );
da_rad = da * PI / 180.0; /* convert to radians */
a_cos = cos(a0_rad);
a_sin = sin(a0_rad);
da_cos = cos(da_rad);
da_sin = sin(da_rad);
printf ( "\n%15s %15s %15s\n", "angle", "cosine", "sine" );
printf ( "--------------- --------------- ---------------\n" );
for ( k=0; k<20; k++ )
{
printf ( "%15.5lf %15.7lf %15.7lf\n", a, a_cos, a_sin );
/* Here's the code that updates the trig values... */
temp = a_cos*da_cos - a_sin*da_sin;
a_sin = a_cos*da_sin + a_sin*da_cos;
a_cos = temp;
/* Update the angle for display purposes. */
/* Note that this step is not needed to update the trig values. */
a += da;
}
return 0;
}
/*--- end of file trig1.c ---*/
|
/* trig2.c - Example program by Don Cross <dcross@intersrv.com> */
/* http://www.intersrv.com/~dcross/fasttrig.html */
#include <stdio.h>
#include <math.h>
#define PI (3.14159265358979323846)
int main (void)
{
double a, da, a0_rad, da_rad;
double a_sin, a_cos, alpha, beta;
double temp;
int k;
printf ( "Enter starting angle in degrees: " );
scanf ( "%lf", &a );
a0_rad = a * PI / 180.0; /* convert to radians */
printf ( "Enter increment angle in degrees: " );
scanf ( "%lf", &da );
da_rad = da * PI / 180.0; /* convert to radians */
a_cos = cos(a0_rad);
a_sin = sin(a0_rad);
alpha = sin(0.5 * da_rad);
alpha = 2.0 * alpha * alpha;
beta = sin(da_rad);
printf ( "\n%15s %15s %15s\n", "angle", "cosine", "sine" );
printf ( "--------------- --------------- ---------------\n" );
for ( k=0; k<20; k++ )
{
printf ( "%15.5lf %15.7lf %15.7lf\n", a, a_cos, a_sin );
/* Here's the code that updates the trig values... */
temp = a_cos - (alpha*a_cos + beta*a_sin);
a_sin = a_sin - (alpha*a_sin - beta*a_cos);
a_cos = temp;
/* Update the angle for display purposes. */
/* Note that this step is not needed to update the trig values. */
a += da;
}
return 0;
}
/*--- end of file trig2.c ---*/
|